Controle PID: rompendo a barreira do tempo

Publicado em 9 de junho de 20208 de junho de 2022 por Roberta Roth

Na história da indústria, por volta do século XVIII, controladores eram utilizados com realimentação mecânica para controle do processo. Geralmente, eles reuniam apenas duas ações do conjunto PID: Proporcional, Integral e Derivativo, mas nunca as três. Naquela época, controlavam a velocidade de acionamento de motores a vapor para proporcionar maior estabilidade no funcionamento de máquinas industriais.

Em 1911, o empreendedor e inventor Elmer Sperry criou o controle PID (Proporcional – Integral – Derivativo), que une as três ações. Sperry desenvolveu este controle para a Marinha dos Estados Unidos com objetivo de automatizar a direção dos navios, a fim de imitar o comportamento de um timoneiro, capaz de compensar variâncias persistentes e prever variações futuras em alto mar. Alguns anos após a criação, o engenheiro Nicolas Minorsky publicou a primeira análise teórica deste controle. Ela descrevia o comportamento em uma equação matemática que até hoje serve como base do cálculo.

Relevância do Controle PID

Atualmente, no ramo empresarial a eficiência é medida em diferentes processos e de várias maneiras. Cada setor possui metas, indicadores e resultados; em cima disso é realizado o controle para obter resultados e buscar a melhor eficiência na utilização de recursos. Para o sistema de produção de uma indústria operar explorando seus limites dentro de um padrão de utilização aceitável, são empregados malhas e algoritmos de controle.

Os controles PID, mesmo com dispositivos mais avançadas disponíveis, são os mais utilizados em malhas de processos nos dias de hoje (BAZANELLA, 2005). É o caso de empresas petroquímicas, de celulose, laticínios ou tratamento de água, entre outras. O fato deste controle, quando bem configurado (modo manual), conseguir antecipar, diminuir e inclusive eliminar ruídos o torna desejável. A configuração manual dos parâmetros PID por vezes exige expertise e embasamento teórico prévio de quem opera. Dessa forma, é possível encontrar encontrar o melhor controle para o seu processo. Segundo Aström; Hägglund (1995), cerca de 90% das malhas de controle em processos industriais operam com este controlador.

Teoria

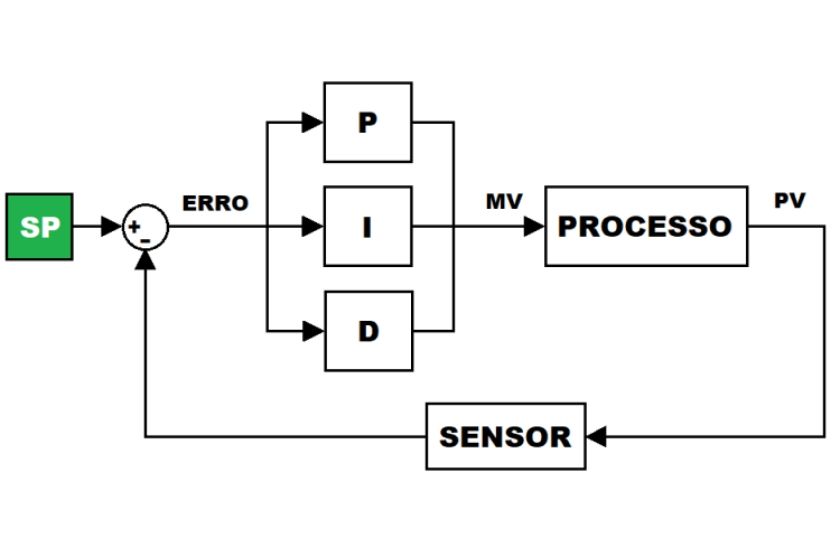
Conhecemos o sistema a ser controlado na indústria como planta ou processo; o sinal aplicado na entrada do processo como sinal de controle ou variável manipulada (MV); e o sinal de saída do processo como variável controlada ou variável de processo (PV). Para alcançar a máxima eficiência da planta, é utilizado um controlador na entrada do processo, que recebe a referência de entrada ou setpoint (SP), e garante a estabilidade do sinal de saída.

Em sistemas com realimentação da saída, é formado um laço no processo. Esta disposição é chamada de malha-fechada. No sistema de malha-fechada o controlador recebe constantemente a diferença entre o SP e o valor real da PV. Esta diferença é chamada de Erro e, com base nela, o equipamento gera um sinal de controle para diminuir o erro a um valor muito pequeno ou nulo (OGATA, 1982), independente se há sinal de perturbação no processo ou não. O controle em malha-fechada proporciona ganhos como aumento da precisão do sistema de controle, rejeição dos efeitos de perturbação sobre PV e diminuição da variação mediante instabilidades (aumenta robustez).

O controle PID une as ações Proporcional, Integral e Derivativo para gerar um só sinal de controle, onde cada ação possui uma forte característica que auxilia no controle da saída. A ação Proporcional faz com que o sistema reaja ao erro presente, possibilitando uma ação imediata diante de variações ou perturbações; a ação Integral elimina erros em regime permanente – em longo prazo – do tipo salto ou degrau, e a ação Derivativa antecipa o comportamento do processo (BAZANELLA, 2005).

Ação Proporcional (Kp)

Existe um limite máximo e mínimo para aplicação do sinal de MV por motivos de restrição de ordem física e segurança: esta faixa de operação é chamada de Banda Proporcional. Se o sinal de controle opera fora dos limites, diz-se que está saturado e opera com comportamento não linear. Quanto maior for o valor da ação Proporcional, menor será a Banda Proporcional e maior a energia de controle. Isto faz com que o sistema responda com maior agilidade, mas o sinal de saída pode ultrapassar ou ficar abaixo do setpoint em regime permanente, e o erro nunca será anulado completamente.

Ação Integral (Ti)

Quando a ação Integral é aplicada de forma isolada, piora a estabilidade relativa do sistema, porém, quando utilizada juntamente com a ação Proporcional, ajuda a anular o erro em regime permanente. Quanto maior o valor da Integral, mais tempo leva para o sistema alcança o setpoint em regime permanente.

Ação Derivativa (Td)

O processo normalmente apresenta uma inércia em relação às modificações na MV, ou seja, o tempo que uma modificação na entrada do processo provoca uma modificação na saída. A ação Derivativa antecipa a ação de controle para que o processo reaja mais rápido do que de costume. Esta ação preditiva aumenta a estabilidade relativa do sistema e torna a resposta mais rápida e menos oscilatória conforme for o tempo derivativo. Em regime permanente esta ação será nula porque o valor de erro será constante.

A equação matemática para cálculo do sinal de controle MV está demonstrada a seguir. Nela estão relacionados os parâmetros Kp, Ti e Td. O valor de Erro, representado como “e” na equação, é utilizado por cada ação de controle para gerar o sinal.

Assim, o controle PID combina as três ações descritas, e cada uma compensa a característica não desejável da outra. A ação Integral em regime permanente torna o erro nulo. Já o efeito oscilatório da ação Integral é suprimido pela ação Derivativa, pois o efeito antecipado torna a resposta mais rápida e aumenta a estabilidade relativa do sistema. A ação Proporcional altera a rapidez com que é buscado o setpoint configurado. Estes comportamentos descritos podem ser observados quando se aumenta o valor de cada ação individualmente no processo.

Conclusão

A relevância do PID continua sendo satisfatória ao longo do tempo pois vários equipamentos para o ramo de automação já são comercializados com este controle como opcional de operação. Atualmente, muitos produtos da NOVUS já vêm com o controle PID como função nativa: conheça estes produtos! Por exemplo, o controlador N1030, controlador N1200, controlador N2000, entre outros. Os controladores NOVUS, além de oferecer ajuste manual dos parâmetros PID também oferecem o recurso de PID autoadaptativo. Portanto, isso quer dizer que são equipamentos que, por meio de testes identificam o processo do cliente e autoconfiguram os melhores valores para o parâmetro Proporcional, Integral e Derivativo em busca de um controle satisfatório.

* Artigo escrito por Lucas Alpi, Analista de Suporte Técnico da NOVUS Automation.

Quer saber mais sobre controladores PID? Veja esse vídeo!