Control PID básico
Este artículo pretende ayudar al lector a crear una percepción física del funcionamiento de un control PID, sin grandes análisis ni rigorismo matemático. Su objetivo es introducir la técnica a los principiantes y mejorar los conocimientos de los ya iniciados, con un enfoque lo más práctico y simplificado posible.
Conceptos preliminares
Algunas definiciones de siglas y términos que se utilizan en este artículo:
- PV: Process Variable o variable de proceso. Variable que es controlada en el proceso, como temperatura, presión, humedad, etc.
- SV o SP: Valor deseado para la variable del proceso.
- MV: Variable manipulada. Variable sobre la que actúa el controlador para controlar el proceso, como la posición de una válvula, la tensión aplicada a una resistencia de calefacción, etc.
- Error o Desviación: Diferencia entre SV y PV. SV-PV para acción inversa y PV-SV para acción directa.
- Acción inversa de control: Puede que sea inversa o directa. Define genéricamente la acción aplicada a la MV en caso de variaciones de PV.
- Acción inversa: Si PV aumenta, MV disminuye. Se utiliza normalmente en controles de calefacción.
- Acción directa: Si PV aumenta, MV aumenta. Se utiliza normalmente en controles de refrigeración.
La técnica de control PID consiste en calcular un valor de acción sobre el proceso a partir de la información del valor deseado y del valor actual de la variable del proceso. Este valor de actuación del proceso se transforma en una señal adecuada para el actuador utilizado (válvula, motor, relé) y debe garantizar un control estable y preciso.
De forma sencilla, el PID se compone de 3 acciones casi intuitivas, que se resumen en el siguiente cuadro:
| P | CORRECCIÓN PROPORCIONAL AL ERROR | La corrección que debe aplicarse al proceso debe crecer en proporción al error entre el valor real y el deseado. |
| I | CORRECCIÓN PROPORCIONAL AL PRODUCTO ERROR x TIEMPO | Los errores pequeños pero de larga duración requieren una corrección más intensiva. |
| D | CORRECCIÓN PROPORCIONAL A LA TASA DE VARIACIÓN DEL ERROR | Si el error varía muy rápidamente, debe reducirse la tasa de cambio para evitar oscilaciones. |
Algo de matemáticas
A continuación se muestra la ecuación PID más habitual:
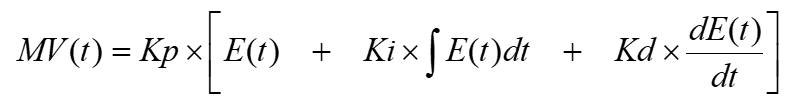
Donde Kp, Ki y Kd son las ganancias de las partes P, I y D y definen la intensidad de cada acción.
Los dispositivos PID de diferentes fabricantes implementan esta ecuación de diferentes maneras. Es habitual adoptar el concepto de «Banda Proporcional» en lugar de Kp, «Tiempo Derivativo» en lugar de Kd y «Tasa Integral» o «Reset» en lugar de Ki, quedando la ecuación de la siguiente manera:
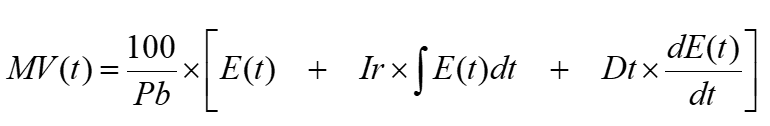
Dónde Pb, Ir y Dt están relacionados con Kp, Ki y Kd y se tratarán individualmente a lo largo de este documento.
Control Proporcional
En el control Proporcional, el valor de MV es proporcional al valor de la desviación (SV-PV, para la acción de control inversa), es decir, para una desviación cero (SV = PV), MV = 0; conforme crece la desviación, MV aumenta hasta un máximo del 100 %. El valor de desviación que lleva la MV al 100 % define la Banda Proporcional (Pb).
Si la Pb es alta, la salida MV sólo asumirá un valor alto para corregir el proceso si la desviación también es alta. Si la Pb es baja, la salida MV asumirá valores altos para corregir el proceso incluso en caso de pequeñas desviaciones. En resumen, cuanto menor sea el valor de Pb, mayor será la acción de control proporcional.
La siguiente figura ilustra el efecto de la variación de Pb en el control de un proceso:
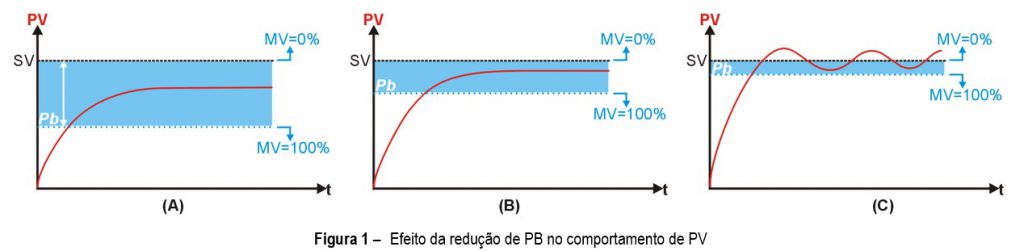
Figura 1 – Efecto de la reducción de Pb sobre el comportamiento de PV
En la Figura 1.A, con la banda proporcional grande, el proceso se estabiliza, pero muy por debajo del Setpoint. Con una disminución de la banda proporcional (Figura 1.B), la estabilización se produce más cerca del Setpoint, pero una reducción excesiva de la banda proporcional (Figura 1.C) puede llevar el proceso a la inestabilidad (oscilación). El ajuste de la banda proporcional forma parte de un proceso denominado Ajuste de control.
Cuando se alcanza la condición deseada (PV = SV), el término proporcional resultará en MV = 0, es decir, no se entregará energía al proceso, lo que provocará de nuevo una desviación. Debido a esto, un control proporcional puro nunca puede estabilizarse con PV = SV.
Muchos controladores que funcionan sólo en modo proporcional añaden un valor constante a la salida de MV para garantizar que, en la condición PV = SV, se suministre algo de energía al sistema (Normalmente el 50 %). Este valor constante se denomina Bias. Cuando es ajustable, permite lograr una estabilización de PV más cercana a SV.
Incluyendo el control integral – PI
La integral no es, aisladamente, una técnica de control, ya que no puede emplearse separadamente de una acción proporcional. La acción integral consiste en una respuesta en la salida del controlador (MV), que es proporcional a la amplitud y duración de la desviación. La acción integral tiene el efecto de eliminar la desviación característica de un control puramente proporcional.
Para entenderlo mejor, imaginemos un proceso estabilizado con control P, según se muestra en la Figura 2.A:
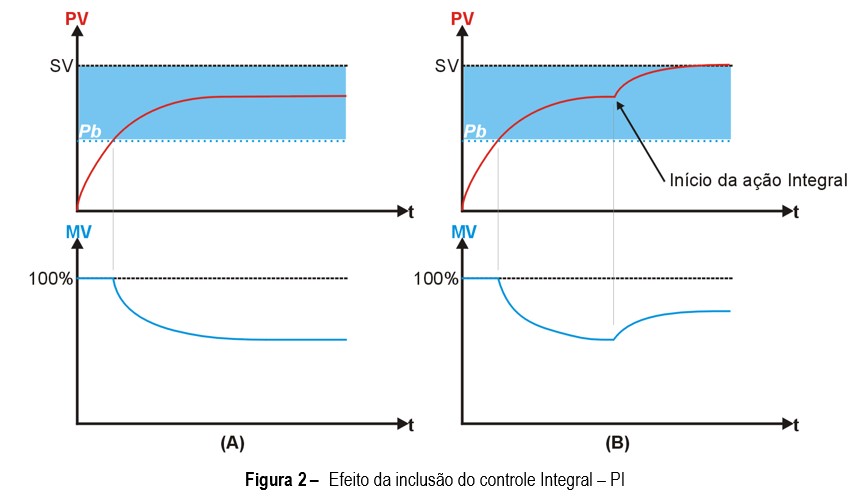
Figura 2 – Efecto de la inclusión del control Integral – PI
En la Figura 2.A, PV y MV alcanzan una condición de equilibrio en la que la cantidad de energía suministrada al sistema (MV) es la necesaria para mantener la PV en el valor en el que se encuentra. En esta circunstancia, si no se produce ninguna perturbación, el proceso permanecerá estable. Aunque estable, el proceso no alcanzó el Setpoint (SV) y se produce el llamado «Error en Régimen Permanente».
Ahora observe la Figura 2.B, donde, en el instante marcado, se ha incluido la acción integral. Observe el aumento gradual del valor de MV y la consiguiente eliminación del error en régimen permanente.
Al incluir la acción integral, el valor de MV se modifica progresivamente para eliminar el error de PV, hasta que PV y MV alcancen un nuevo equilibrio, pero ahora con PV = SV.
La acción integral funciona de la siguiente manera: A intervalos regulares, la acción integral corrige el valor de la MV, añadiéndole el valor de la desviación SV-PV. Este intervalo de actuación se denomina Tiempo Integral, que también puede expresarse por su inverso, denominado Tasa Integral (Ir). Al aumentar la Tasa Integral (Ir), aumenta el rendimiento de la Integral en el control del proceso.
La única finalidad de la acción integral es eliminar el error en régimen permanente. La adopción de un término integral que actúe en exceso puede llevar el proceso a la inestabilidad. Al adoptar una integral que actúa débilmente, se retrasa demasiado la estabilización PV = SV.
Incluyendo el control derivativo – PD
El derivativo no es, aisladamente, una técnica de control, ya que no puede emplearse separadamente de una acción proporcional. La acción derivada consiste en una respuesta en la salida del controlador (MV), que es proporcional a la amplitud y duración de la desviación. La acción derivativa tiene el efecto de reducir la velocidad de las variaciones de PV, evitando que suban o bajen demasiado rápido.
El derivativo sólo actúa cuando hay variación en el error. Si el proceso es estable, su efecto es nulo. Durante las perturbaciones o en el arranque del proceso, cuando el error es variable, el derivativo actúa siempre en el sentido de atenuar las variaciones, por lo que su función principal es mejorar el rendimiento del proceso durante los transitorios.
La Figura 3 compara respuestas hipotéticas de un proceso con control P (A) y PD (B):
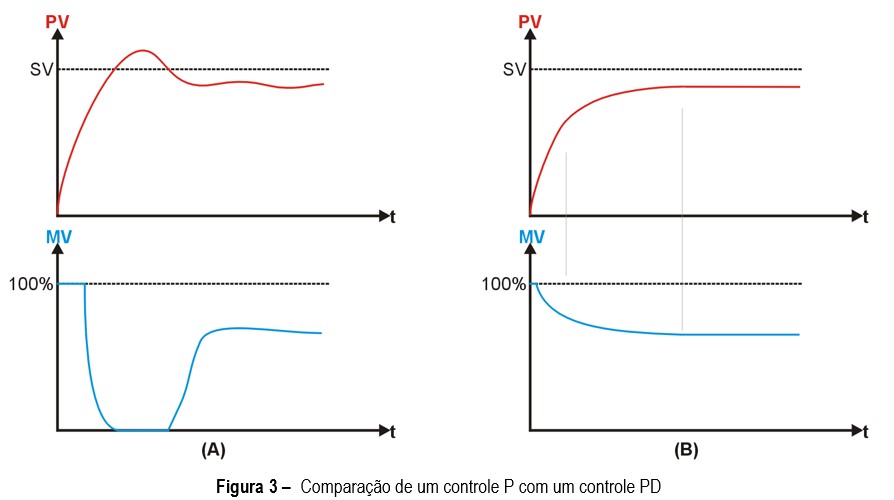
Figura 3 – Comparación de un control P con un control PD
En el control P (Figura 3.A), si la banda proporcional es pequeña, es muy probable que se produzca un «overshoot«, en el que PV sobrepasa a SV antes de estabilizarse. Esto se debe al tiempo prolongado que MV estuvo en su valor máximo y a que su reducción comenzó muy cerca de SV, cuando ya es demasiado tarde para evitar el overshoot.
Una solución sería aumentar la banda proporcional, pero esto aumentaría el error en régimen permanente. Otra solución es incluir el control derivativo (Figura 3.B), que reduce el valor de MV si PV crece muy rápidamente. Al anticipar la variación de PV, la acción derivada reduce o elimina el overshoot y las oscilaciones en el periodo transitorio del proceso.
Matemáticamente, la contribución del derivativo en el control se calcula de la siguiente manera: En intervalos regulares, el controlador calcula la variación de la desviación del proceso, sumando a la MV el valor de esta variación. Si PV está aumentando, la desviación se reduce, lo que resulta en una variación negativa, que reduce el valor de MV y, por consecuencia, tarda la elevación de PV. Se ajusta la intensidad de la acción derivada, cambiando el intervalo de cálculo de la diferencia. Este parámetro se llama Tiempo Derivativo (Dt). El aumento del valor de Dt aumenta la acción derivada, reduciendo la velocidad de variación de PV.
Control PID
Al unir las 3 técnicas, es posible juntar el control básico de P con la eliminación del error de I y la reducción de oscilaciones de D, pero se crea la dificultad de ajustar la intensidad de cada uno de los términos, proceso denominado ajuste del PID.
>>>> Consulte la siguiente publicación para obtener más información sobre el ajuste y el autoajuste de PID.
Controlador PID: conozca los controladores NOVUS con esta función
Lea también:
Cómo elegir un controlador de procesos para su aplicación
















