Controle PID básico

Publicado em 3 de abril de 202326 de março de 2024 por Roberta Roth

Este artigo pretende ajudar o leitor a criar uma percepção física do funcionamento de um controle PID, sem grandes análises e rigorismos matemáticos. Ele visa introduzir a técnica aos iniciantes e aprimorar o conhecimento dos já iniciados, com a abordagem mais prática e simplificada possível.

NOÇÕES PRELIMINARES

Algumas definições de siglas e termos utilizados neste artigo:

PV: Process Variable ou variável de processo. Variável que é controlada no processo, como temperatura, pressão, umidade, etc.
SV ou SP: Setpoint. Valor desejado para a variável de processo.
MV: Variável manipulada. Variável sobre a qual o controlador atua para controlar o processo, como posição de uma válvula, tensão aplicada a uma resistência de aquecimento, etc.
Erro ou Desvio: Diferença entre SV e PV. SV-PV para ação reversa e PV-SV para ação direta.
Ação de controle: Pode ser reversa ou direta. Define genericamente a atuação aplicada à MV na ocorrência de variações da PV.
Ação Reversa: Se PV aumenta, MV diminui. Tipicamente utilizada em controles de aquecimento.
Ação Direta: Se PV aumenta, MV aumenta. Tipicamente utilizada em controles de refrigeração.

A técnica de controle PID consiste em calcular um valor de atuação sobre o processo a partir das informações do valor desejado e do valor atual da variável do processo. Este valor de atuação sobre o processo é transformado em um sinal adequado ao atuador utilizado (válvula, motor, relé) e deve garantir um controle estável e preciso.

De uma maneira bem simples, o PID é composto por 3 ações quase intuitivas, conforme resume o quadro a seguir:

P	CORREÇÃO PROPORCIONAL AO ERRO	A correção a ser aplicada ao processo deve crescer na proporção que cresce o erro entre o valor real e o desejado.
I	CORREÇÃO PROPORCIONAL AO PRODUTO ERRO x TEMPO	Erros pequenos, mas que existem há muito tempo requerem correção mais intensa.
D	CORREÇÃO PROPORCIONAL À TAXA DE VARIAÇÃO DO ERRO	Se o erro está variando muito rápido, esta taxa de variação deve ser reduzida para evitar oscilações.

Um pouco de matemática

A equação mais usual do PID é apresentada a seguir:

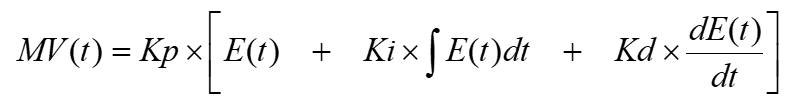
Onde Kp, Ki e Kd são os ganhos das parcelas P, I e D e definem a intensidade de cada ação.

Equipamentos PID de diferentes fabricantes implementam essa equação de diferentes maneiras. É usual adotar o conceito de “Banda Proporcional” em substituição a Kp, “Tempo derivativo” em substituição a Kd e “Taxa Integral” ou “Reset” em substituição a Ki, ficando a equação da seguinte forma:

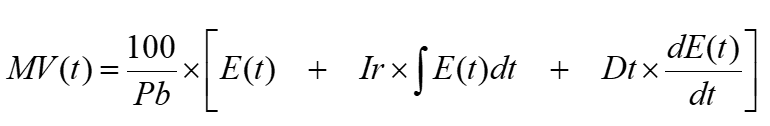
Onde Pb, Ir e Dt estão relacionados a Kp, Ki e Kd e serão individualmente abordados ao longo deste artigo.

Controle Proporcional

No controle Proporcional, o valor de MV é proporcional ao valor do desvio (SV-PV, para ação reversa de controle), ou seja, para desvio zero (SV = PV), MV = 0; à medida que o desvio cresce, MV aumenta até o máximo de 100 %. O valor de desvio que provoca MV = 100 % define a Banda Proporcional (Pb).

Com Pb alta, a saída MV só irá assumir um valor alto para corrigir o processo se o desvio for alto. Com Pb baixa, a saída MV assumirá valores altos para corrigir o processo mesmo em caso de pequenos desvios. Em resumo, quanto menor o valor de Pb, mais forte será a ação proporcional de controle.

A figura a seguir ilustra o efeito da variação de Pb no controle de um processo:

Na Figura 1.A, com a banda proporcional grande, o processo estabiliza, porém muito abaixo do Setpoint. Com a diminuição da banda proporcional (Figura 1.B), a estabilização ocorre mais próxima do Setpoint, mas uma redução excessiva da banda proporcional (Figura 1.C) pode levar o processo à instabilidade (oscilação). O ajuste da banda proporcional faz parte de um processo chamado de Sintonia do controle.

Quando a condição desejada (PV = SV) for atingida, o termo proporcional resultará em MV = 0, ou seja, nenhuma energia será entregue ao processo, o que fará com que volte a surgir um desvio. Por causa disso, um controle proporcional puro nunca consegue se estabilizar com PV = SV.

Muitos controladores que operam apenas no modo Proporcional adicionam um valor constante à saída de MV para garantir que, na condição PV = SV, alguma energia seja entregue ao sistema (Tipicamente 50 %). Esse valor constante é denominado Bias (polarização). Quando ajustável, ele permite obter uma estabilização de PV mais próxima a SV.

Incluindo o controle integral – PI

O integral não é, isoladamente, uma técnica de controle, pois não pode ser empregado em separado de uma ação proporcional. A ação integral consiste em uma resposta na saída do controlador (MV), que é proporcional à amplitude e duração do desvio. A ação integral tem o efeito de eliminar o desvio característico de um controle puramente proporcional.

Para compreender melhor, imagine um processo estabilizado com controle P, conforme apresentado na Figura 2.A:

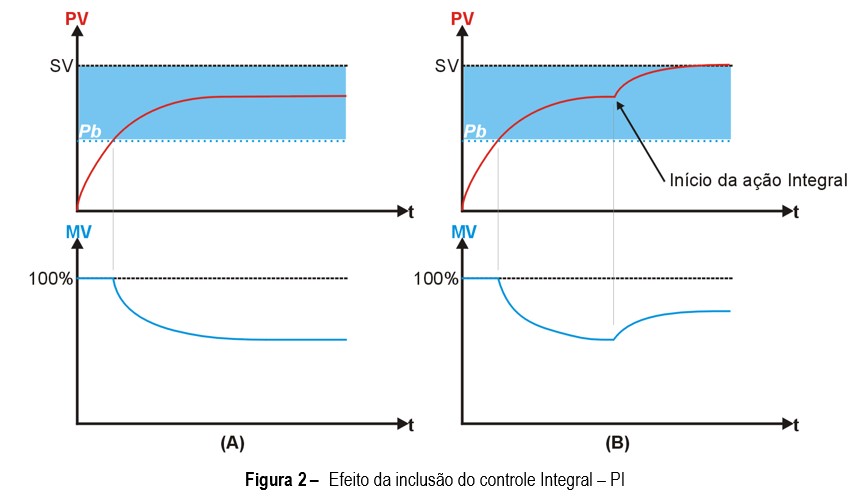
Na Figura 2.A, PV e MV atingem uma condição de equilíbrio em que a quantidade de energia entregue ao sistema (MV) é a necessária para manter PV no valor em que ela está. Nessa condição, se não ocorrer nenhuma perturbação, o processo irá permanecer estável. Apesar de estável, o processo não atingiu o Setpoint (SV), existindo o chamado Erro em Regime Permanente.

Agora observe a Figura 2.B, onde, no instante assinalado, foi incluída a ação integral. Observe a gradual elevação do valor de MV e a consequente eliminação do erro em regime permanente. Com a inclusão da ação integral, o valor de MV é alterado de modo progressivo, no sentido de eliminar o erro de PV, até que PV e MV alcancem um novo equilíbrio, mas agora com PV = SV.

A ação integral funciona da seguinte maneira: A intervalos regulares, a ação integral corrige o valor de MV, somando a esta o valor do desvio SV-PV. Esse intervalo de atuação se chama Tempo Integral, que também pode ser expresso por seu inverso, chamado Taxa Integral (Ir). O aumento da Taxa Integral (Ir) aumenta a atuação do Integral no controle do processo.

A ação integral tem como único objetivo eliminar o erro em regime permanente. A adoção de um termo integral excessivamente atuante pode levar o processo à instabilidade. A adoção de um integral pouco atuante retarda em demasia a estabilização PV = SV.

Incluindo o controle derivativo – PD

O derivativo não é, isoladamente, uma técnica de controle, pois não pode ser empregado separado de uma ação proporcional. A ação derivativa consiste em uma resposta na saída do controlador (MV), que é proporcional à velocidade de variação do desvio. A ação derivativa tem o efeito de reduzir a velocidade das variações de PV, evitando que se eleve ou reduza muito rapidamente.

O derivativo só atua quando há variação no erro. Se o processo está estável, seu efeito é nulo. Durante perturbações ou na partida do processo, quando o erro está variando, o derivativo sempre atua no sentido de atenuar as variações, sendo, portanto, sua principal função melhorar o desempenho do processo durante os transitórios.

A Figura 3 compara respostas hipotéticas de um processo com controle P (A) e PD (B):

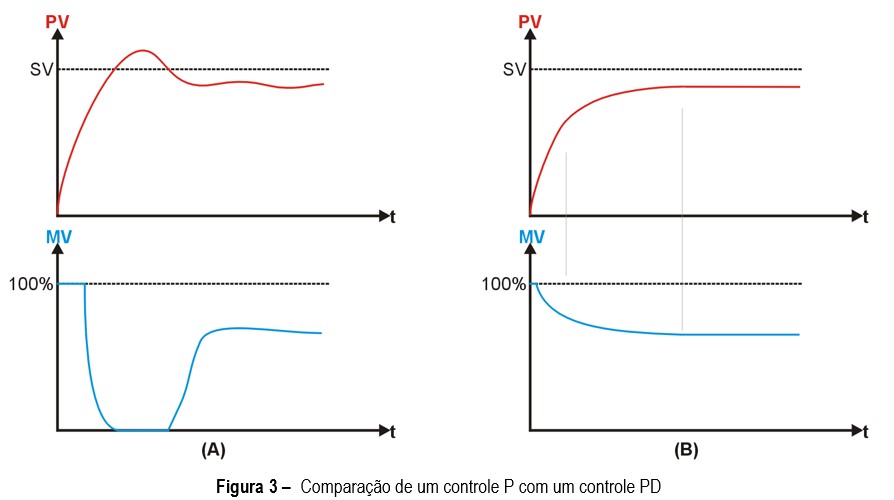
No controle P (Figura 3.A), se a banda proporcional é pequena, é bem provável que ocorra um “overshoot“, onde PV ultrapassa SV antes de estabilizar. Isso ocorre pelo longo tempo em que MV esteve no seu valor máximo e por ter sua redução iniciada já muito próxima de SV, quando já é tarde para impedir o overshoot.

Uma solução seria aumentar a banda proporcional, mas isso aumentaria o erro em regime permanente. Outra solução é incluir o controle derivativo (Figura 3.B), que reduz o valor de MV caso PV esteja crescendo muito rápido. Ao antecipar a variação de PV, a ação derivativa reduz ou elimina o overshoot e as oscilações no período transitório do processo.

Matematicamente, a contribuição do derivativo no controle é calculada da seguinte maneira: A intervalos regulares, o controlador calcula a variação do desvio do processo, somando à MV o valor desta variação. Se PV está aumentando, o desvio está reduzindo, o que resulta em uma variação negativa, que reduz o valor de MV e, consequentemente, retarda a elevação de PV. A intensidade da ação derivativa é ajustada, variando-se o intervalo de cálculo da diferença. Este parâmetro é chamado de Tempo Derivativo (Dt). O aumento do valor de Dt aumenta a ação derivativa, reduzindo a velocidade de variação de PV.

Controle e sintonia do PID

Ao unir as 3 técnicas, conseguimos unir o controle básico do P com a eliminação do erro do I e a redução de oscilações do D, mas se cria a dificuldade de ajustar a intensidade da cada um dos termos, processo chamado de sintonia do PID.

>>>>>>> Veja o próximo post para saber mais sobre sintonia do PID e autotune.

Controlador PID: conheça os controladores NOVUS com esta função